Drawing Shapes

Drawing 2D and 3D shapes to a window using openFrameworks is a snap.

Table of Contents

  1. The Canvas
  2. Canvas Size
  3. Drawing Lines in 2D
  4. Drawing 2D Shapes
  5. Drawing 3D Shapes
  6. Colour
  7. ofColor Class
  8. Shape Fill
  9. Background Colour
  10. Translation, Rotation, and Scaling

The Canvas

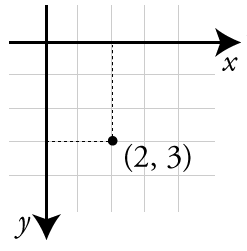
Canvas Coordinates

When working in 2D, the canvas can be consider to be a grid of pixels. This is similar to the x/y cartesian coordinates used in high-school algebra, but with a few changes:

  • The origin (where x and y are zero) is in the top left corner of the screen.
  • The y-axis is flipped such that values of y increase as you go down the screen.

The image to the right shows a dot at x = 2 and y = 3.

Canvas Size

By default, the size of the canvas is 1024 (width) by 768 (height) pixels. The size of the canvas can be changed by resizing the application window, or in the main.cpp file:

ofSetupOpenGL(1024, 768, OF_WINDOW); // 1024x768 Windowed
ofSetupOpenGL(1024, 768, OF_FULLSCREEN); // 1024x768 Full Screen

The size and position of the canvas can also be changed from within ofApp:setup():

ofSetWindowShape(500, 500);
ofSetWindowPosition(10, 10);

Because the canvas can be resized while your app is running, there are methods to fetch the current width and height:

int width = ofGetWidth();
int height = ofGetHeight();

Drawing Lines in 2D

We can draw a line between any two points on the canvas:

ofSetLineWidth(5); // If not set, defaults to a thickness of 1.
ofDrawLine(0, 0, ofGetWidth(), ofGetHeight()); // Line from top left to bottom right corners.

For anti-aliased lines we need to the following to setup():

ofEnableSmoothing();

Resources

Drawing 2D Shapes

There are a number of methods that allow you to draw 2D shapes to the canvas:

Resources

Drawing 3D Shapes

There are a number of methods that allow you to draw 2D shapes to the canvas:

Resources

Colour

The color of the lines and shapes you draw is set using ofSetColor():

ofSetColor(200); // Greyscale color from 0 (black) to 255 (white).
ofSetColor(255, 0, 0); // R, G, B values from 0 to 255.

Alpha blending can be enabled to create colours with a 0-255 level of transparency, where 0 is fully transparent and 255 is fully opaque.

ofEnableAlphaBlending(); // With Alpha Blending enable we can make transparent colours.
ofSetColor(255,0,0,127); // Red, 50% transparent
ofDrawRectangle(20,20,100,100);
ofDisableAlphaBlending(); // Disable if you don't need alpha any more.

Resources

ofColor Class

There’s also an ofColor data type, which includes a bunch of predefined colors:

// ofColor object configured using r/g/b properties:
ofColor red;
red.r=255;
red.g=0;
red.b=0;
ofSetColor(red);
// ofColor created using a constructor:
ofColor green(0, 255, 0, 255);
ofSetColor(green);
// Using a pre-defined color by name:
ofSetColor(ofColor::fuchsia);

There’s much more to ofColor like lerping, inverting colors, or working in the HSB color space.

Resources

Shape Fill

By default, all shapes are drawn filled in, but this can be disable/enable.

ofSetColor(0,0,255);
ofNoFill();
ofDrawRectangle(10,10,100,100);  //draws only the rectangle outline in blue
ofFill();
ofDrawRectangle(200,200,100,100);  //draws the rectangle filled in blue

Background Colour

The canvas is automatically cleared with a background color once each frame before the draw() method is called. The background color can be set using:

ofBackground(50); // Greyscale from black (0) to white (255)
ofBackground(50, 200); // Greyscale with alpha channel
ofBackground(ofColor::blue); // Using an ofColor
ofBackground(50, 90, 200, 255); // R, G, B, A (0-255)

A gradient background can also be set:

ofColor colorOne(255, 0, 0);
ofColor colorTwo(0, 0, 255);
// Circular gradient from red (inner) to blue (outer).
ofBackgroundGradient(colorOne, colorTwo, OF_GRADIENT_CIRCULAR);
// Linear gradient from red (top) to blue (bottom).
ofBackgroundGradient(colorOne, colorTwo, OF_GRADIENT_LINEAR);
// Three part linear gradient from red (top) to blue (middle) back to red (bottom).
ofBackgroundGradient(colorOne, colorTwo, OF_GRADIENT_BAR);

Sometimes you don’t want the background to automatically clear. The automatic clearing can be disabled/enabled like this:

ofSetBackgroundAuto(false); // Disable automatic background clearing.
ofSetBackgroundAuto(true); // Enable automatic background clearing.

Translation, Rotation, and Scaling

We can change the position, scale, and rotation of the coordinate system using a variety of translate and rotate methods. These operations work when drawing shapes in 2D and 3D.

ofTranslate(200, 200, 0); // Move the origin to (200, 200)
ofRotateZDeg(45); // Rotate coordinate system by 45 degree (around z)
ofDrawRectangle(0, 0, 100, 100); // Draw a diamond.

We can also save and restore the state of the coordinate system using ofPushMatrix() and ofPopMatrix().

ofPushMatrix(); // Save the original unrotated coordinate system with origin top left.
ofTranslate(200, 200, 0); // Move the origin to (200, 200)
ofRotateZDeg(45); // Rotate coordinate system by 45 degree (around z)
ofScale(2, 2); // Double the scale.
ofDrawRectangle(0, 0, 100, 100); // Draw a diamond.
ofPopMatrix(); // Restore the original coordinate system.
ofDrawRectangle(0, 0, 100, 100); // Draw a square in the top left corner.

⚡ Warning:

ofScale() scales the coordinate system but does not affect shape stroke weight.

Resources