Different Types of Numbers

In mathematics there are different types of numbers, each with a unique place in the numeric family tree.

Table of Contents

  1. A Family Tree of Numbers
  2. Visual Subsets of Numbers
  3. Number Types Videos
  4. Further Reading

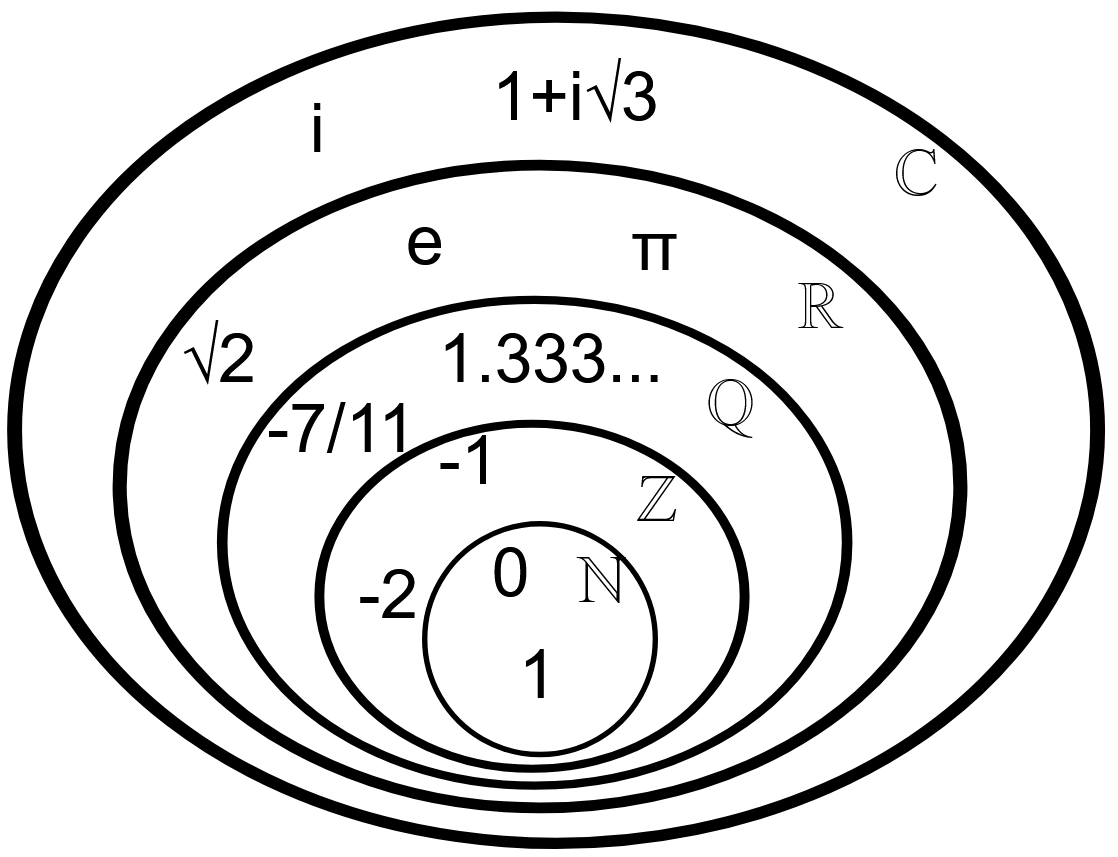
A Family Tree of Numbers

Let’s start by defining the different categories of numbers:

  • Natural Numbers: Also known as the counting numbers, these are the positive integers starting at 1. β„• = {1, 2, 3, 4, …}
  • Whole Numbers: The natural numbers, but including zero. π•Ž = {0, 1, 2, 3, 4, …}
  • Integers: The whole numbers, but including all negative versions. β„€ = { …, -3, -2, -1, 0, 1, 2, 3, …}
  • Rational Numbers: Any number that can be written as a ratio of two numbers in the form p/q, where both p and q are natural numbers. β„š is used represent the rationals.
  • Irrational Numbers: Any number that cannot be expressed as the ratio of one over another. These numbers where their fractional component extends forever in a non-repeating sequence. ℝ-β„š is sometimes used to represent the irrationals. Examples include Ο€ and the square root of 2.
  • Real Numbers: Any number that can represent a distance on a number line. The reals (ℝ) include all integer, rational, and irrational numbers.
  • Imaginary Numbers: Numbers that are the product of a real number and the imaginary unit i, where i is defined to be the square root of -1.
  • Complex Numbers: Number of the form a+bi where β€œa and b” are real numbers and β€œi” is the imaginary unit defined above. The set of all complex numbers is represented by β„‚s.

Visual Subsets of Numbers

Subsets of Numbers from https://en.wikipedia.org/wiki/Number

🎡 Note:

Image combines the whole numbers (π•Ž) with the natural numbers (β„•).

Number Types Videos

A slightly different way of looking at this (without the inclusion of the imaginary numbers):

Further Reading